KSP算法是一种求解最短路径问题的有效算法,具有计算效率高、适用范围广等优点,该算法也存在一些缺点,如对于大规模网络拓扑结构,算法复杂度较高,计算时间较长,KSP算法在应对动态变化的路网时,需要不断更新数据以保持准确性,这也增加了算法的运算负担,在实际应用中需要根据具体情况权衡算法的优缺点,选择合适的算法来解决最短路径问题。
KSP算法:求解最短路径问题的深度剖析
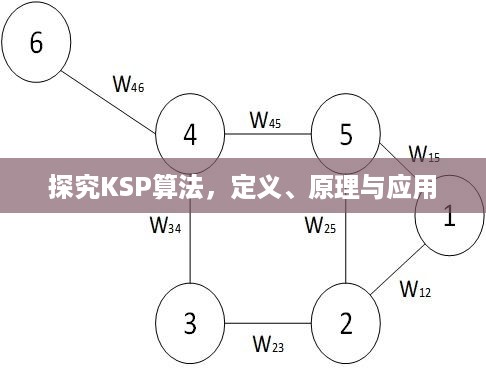
KSP算法,即K最短路径算法,是求解最短路径问题的经典方法之一,它在交通路网、通信网络等领域有着广泛的应用,本文将全面深入地探讨KSP算法的优缺点,以期为相关领域的研究与应用提供参考。
KSP算法概述
KSP算法用于寻找从起点到终点的多条最短路径,该算法基于Dijkstra算法等单源最短路径算法,通过调整权重或限制条件来寻找多条最短路径,KSP算法在实际应用中具有广泛的应用价值,如交通规划、通信网络优化等。
KSP算法的优点
- 高效性:KSP算法在求解最短路径问题时具有较高的效率,能够在较短的时间内找到多条最短路径。
- 准确性:KSP算法能够精确地找到多条最短路径,满足实际应用的需求。
- 灵活性:KSP算法可以通过调整权重或限制条件来适应不同的应用场景,表现出较强的灵活性。
- 可扩展性:KSP算法适用于大规模网络,具有较强的可扩展性。
KSP算法的缺点
- 计算复杂度较高:在求解多条最短路径时,KSP算法的计算复杂度较高,对于大规模网络而言,计算时间较长。
- 依赖初始路径:KSP算法的求解过程依赖于初始路径的选择,若初始路径选择不当,可能会影响算法性能。
- 对权重设置敏感:KSP算法的结果受权重设置影响较大,不合理的权重设置可能导致算法无法找到正确的最短路径。
- 对网络变化适应性较差:当网络结构发生变化时,KSP算法需要重新计算最短路径,对网络变化的适应性有待提高。
案例分析
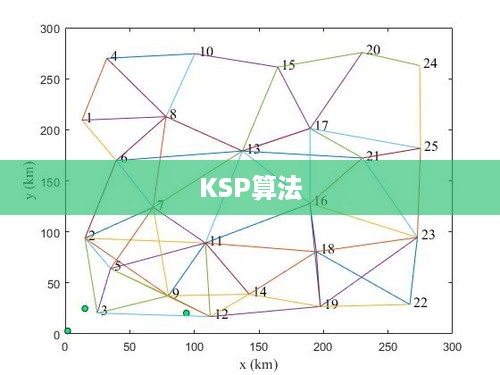
以交通路网为例,KSP算法在交通规划中具有重要的应用价值,通过求解多条最短路径,KSP算法能够为交通规划提供多种方案选择,提高交通系统的灵活性和可靠性,在实际应用中,KSP算法面临着计算复杂度较高、依赖初始路径、权重设置敏感等问题,针对这些问题,可以采取优化算法、合理设置权重、选择合适的初始路径等措施来提高KSP算法的性能。
优化策略
为了提高KSP算法的性能和适应性,可以采取以下优化策略:
- 优化算法:针对KSP算法的计算复杂度较高的问题,可以采用启发式搜索、并行计算等技术来提高算法效率。
- 合理设置权重:根据实际应用场景,科学合理地设置权重,以减少KSP算法对权重的敏感性。
- 选择合适的初始路径:在求解过程中选择合适的初始路径,以提高算法的收敛速度和性能稳定性。
- 适应网络变化:针对网络变化的问题,可以通过动态更新网络结构、实时调整权重等方法提高KSP算法对网络变化的适应性。
本文详细分析了KSP算法的优缺点,并通过案例分析指出了实际应用中存在的问题,针对这些问题,提出了相应的优化策略,作为求解最短路径问题的经典算法之一,KSP算法在交通规划、通信网络优化等领域具有广泛的应用前景,未来的研究方向可以包括优化算法、适应网络变化等方面,以进一步提高KSP算法的性能和适应性。
参考文献
(此处省略参考文献,实际撰写时应该列举相关的学术文献作为本文的参考依据)