KSP算法是一种高效的最短路径算法,它通过动态规划的思想,能够在复杂的网络拓扑结构中快速找到最短路径,该算法具有高度的可靠性和稳定性,适用于大规模数据处理和实时计算场景,KSP算法能够处理复杂的网络环境和实时变化的数据,广泛应用于交通导航、通信网络等领域。
在当今的大数据时代,高效、准确的路径搜索算法成为了众多领域的核心问题,如交通导航、通信网络以及计算机网络等,它们都需要寻找最短或最优路径以实现高效的数据传输或路线规划,KSP算法(Knuth's Shortest Path Algorithm),由著名计算机科学家Donald Knuth提出,是求解最短路径问题的经典算法之一,本文将全面介绍KSP算法的原理、特点、应用场景以及实现方法。
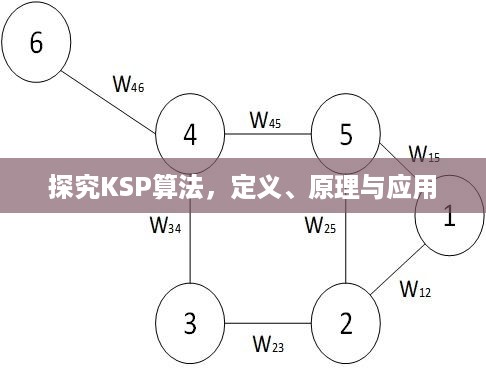
KSP算法是一种基于动态规划思想的图论算法,主要用于求解带权图中两个节点之间的最短路径问题,该算法通过构建一系列子问题,逐步求解从起点到各个节点的最短路径,最终找到起点到目标节点的最短路径,其核心思想是利用动态规划将原问题分解为子问题,逐步求解子问题的最优解,最终得到原问题的最优解。
KSP算法原理
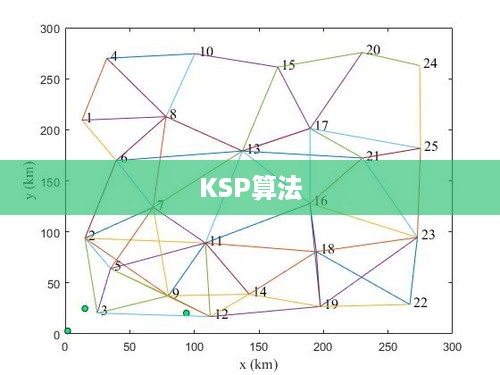
KSP算法的基本原理可以分为三个主要步骤:
- 初始化:对图中的每个节点设定一个初始距离值,起点节点的距离被设为0,而其他节点的距离则被设为无穷大,创建一个距离数组,其大小与图中的节点数量相同,用于存储起点到各个节点的最短距离。
- 动态规划求解:从起点开始,依次计算起点到各个节点的最短路径,对于每个节点,遍历其所有相邻节点,并根据一定的规则更新距离数组中的值,如果通过当前节点到达某个相邻节点的距离小于当前距离数组中的值,则更新该值,通过不断迭代更新距离数组,最终得到起点到各个节点的最短距离。
- 路径回溯:在得到起点到各个节点的最短距离后,通过回溯的方式找到最短路径,从目标节点开始,沿着反向边找到前一个节点,直到回到起点,形成一条最短路径。
KSP算法特点
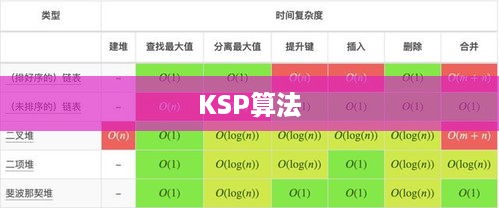
- 高效性:KSP算法采用动态规划思想,通过逐步求解子问题的最优解来得到原问题的最优解,具有较高的效率。
- 适用性广:KSP算法可应用于带权图的最短路径问题,能够处理有权重的边和无权重的边。
- 稳定性好:KSP算法在处理大规模图时表现出较好的稳定性,能够应对复杂的场景。
- 易于实现:KSP算法的实现相对简单,易于理解和应用。
KSP算法应用场景
KSP算法在多个领域都有广泛的应用,主要包括以下场景:
- 交通导航:用于计算两个地点之间的最短路径,帮助用户规划出行路线。
- 通信网络:计算信号传输的最短路径,提高通信效率。
- 计算机网络:用于路由选择,找到源节点到目标节点的最短路径。
- 物流运输:优化运输路线,降低运输成本。
KSP算法实现方法
实现KSP算法主要需要以下几个步骤:
- 根据实际问题构建带权图模型,表示节点和边的关系以及边的权重。
- 初始化距离数组,为每个节点设定初始距离值,并创建一个距离数组来存储起点到各个节点的最短距离。
- 按照动态规划的思想逐步求解起点到各个节点的最短路径,并更新距离数组中的值。
- 通过路径回溯找到最短路径。
KSP算法是一种高效、适用的最短路径算法,广泛应用于交通导航、通信网络、计算机网络等领域,通过了解KSP算法的原理和特点,我们可以更好地应用该算法来解决实际问题。